Теория хаоса представляет собой революционный подход к пониманию сложных систем, где малейшие изменения могут привести к кардинально разным результатам. В современном мире, где мы постоянно сталкиваемся с неопределенностью — от колебаний финансовых рынков до изменений погоды в Казахстане — понимание принципов хаотических систем становится критически важным.
Эта наука изучает поведение динамических систем, которые крайне чувствительны к начальным условиям. Парадокс заключается в том, что детерминированные системы (где каждое состояние определяется предыдущим) могут демонстрировать абсолютно непредсказуемое поведение. В данной статье мы разберем фундаментальные принципы теории хаоса, методы анализа случайных событий и практические применения этих знаний.
Вы узнаете, как работают хаотические системы, почему некоторые процессы невозможно предсказать на длительный период, и какие современные инструменты помогают находить закономерности в кажущемся беспорядке.

Основы теории хаоса: от порядка к непредсказуемости
Теория хаоса зародилась в 1960-х годах благодаря работам метеоролога Эдварда Лоренца, который случайно обнаружил чувствительность погодных моделей к начальным условиям. Это открытие кардинально изменило наше понимание детерминизма в науке.
Детерминированный хаос: парадокс предсказуемости
Детерминированные системы подчиняются строгим математическим законам, где каждое последующее состояние однозначно определяется предыдущим. Однако даже такие системы могут демонстрировать хаотическое поведение. Классический пример — система трех тел в механике, где взаимодействие трех объектов под действием гравитации приводит к непредсказуемым траекториям.
Ключевые характеристики детерминированного хаоса:
- Чувствительная зависимость от начальных условий
- Наличие странных аттракторов в фазовом пространстве
- Фрактальная структура траекторий
- Перемешивание и топологическая транзитивность
- Периодические орбиты плотно распределены в пространстве
Математические основы хаотических систем
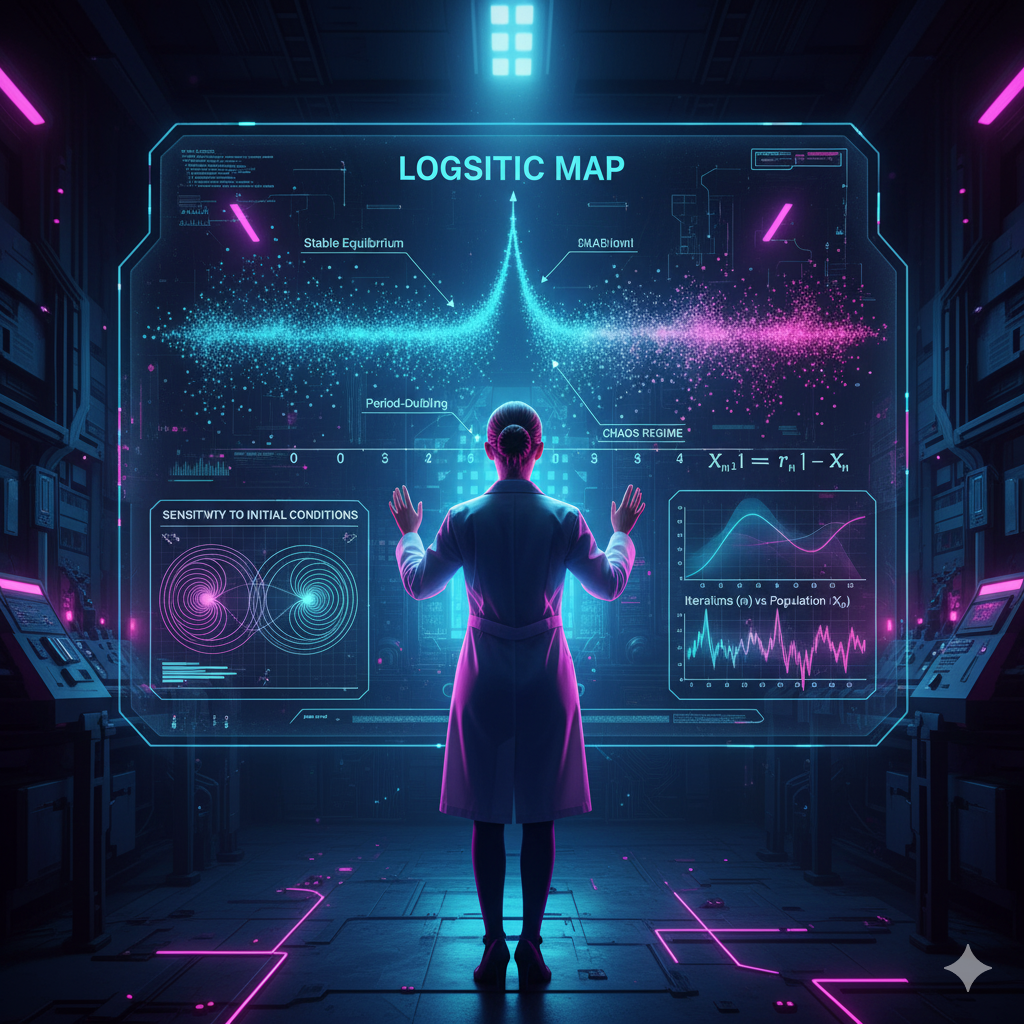
Хаотические системы описываются нелинейными дифференциальными уравнениями. Простейший пример — логистическое отображение:
x(n+1) = r × x(n) × (1 — x(n))
При различных значениях параметра r система демонстрирует переход от устойчивого равновесия через удвоение периода к полному хаосу. Это явление называется сценарием Фейгенбаума и универсально для многих нелинейных систем.
| Значение r | Поведение системы | Характеристика |
|---|---|---|
| 0 < r < 1 | Вымирание | Стремление к нулю |
| 1 < r < 3 | Стабильное состояние | Единственная неподвижная точка |
| 3 < r < 3.57 | Периодические колебания | Удвоение периода |
| r > 3.57 | Хаотическое поведение | Непредсказуемая динамика |
Эффект бабочки и чувствительность к начальным условиям
Эффект бабочки — метафорическое название явления, при котором малейшие изменения в одной части системы могут привести к кардинальным изменениям в другой части. Лоренц образно описал это как возможность того, что взмах крыльев бабочки в Бразилии может вызвать торнадо в Техасе.
Практические проявления чувствительности
В реальной жизни эффект бабочки проявляется во множестве областей:
- Метеорология: Невозможность точного долгосрочного прогноза погоды. В Казахстане, например, прогноз на неделю имеет точность около 65%, а на месяц — менее 30%
- Финансовые рынки: Небольшие новости могут вызвать значительные колебания цен на KASE (Казахстанская фондовая биржа)
- Экосистемы: Исчезновение одного вида может кардинально изменить всю пищевую цепь
- Социальные системы: Малые события могут запускать крупные социальные изменения
Количественная оценка чувствительности
Чувствительность к начальным условиям измеряется через показатели Ляпунова. Положительный показатель Ляпунова указывает на экспоненциальное расхождение близких траекторий, что является математическим определением хаоса.
Для системы с показателем Ляпунова λ > 0, расстояние между двумя изначально близкими траекториями растет как:
δ(t) = δ₀ × e^(λt)
Это означает, что даже микроскопическая погрешность в измерениях со временем приведет к полной непредсказуемости системы.

Странные аттракторы и фрактальная геометрия
Аттракторы представляют собой множества в фазовом пространстве, к которым стремятся траектории динамической системы. Странные аттракторы характерны для хаотических систем и обладают фрактальной структурой — они имеют дробную размерность и самоподобие на разных масштабах.
Знаменитые странные аттракторы
Аттрактор Лоренца — классический пример странного аттрактора, возникающий в упрощенной модели конвекции. Его форма напоминает бабочку и демонстрирует основные свойства хаотических систем:
- Траектории никогда не пересекаются
- Система остается в ограниченной области пространства
- Поведение непериодическое и непредсказуемое
- Фрактальная размерность около 2.06
Другие важные примеры включают аттрактор Рёсслера, аттрактор Чуа и аттрактор Дуффинга. Каждый из них демонстрирует уникальные свойства и находит применение в различных областях науки и техники.
Фрактальные свойства и размерность
Фрактальная размерность странных аттракторов является нецелым числом, что отражает их сложную геометрическую структуру. Методы вычисления включают:
- Размерность Хаусдорфа: Теоретическая мера, основанная на покрытии множества
- Корреляционная размерность: Практический метод, основанный на анализе корреляций
- Информационная размерность: Учитывает распределение вероятности на аттракторе
- Размерность Ляпунова: Связана с показателями Ляпунова системы
| Тип аттрактора | Размерность | Примеры |
|---|---|---|
| Точечный | 0 | Устойчивое равновесие |
| Предельный цикл | 1 | Периодические колебания |
| Тор | 2 | Квазипериодические движения |
| Странный | Дробная | Хаотическая динамика |
Методы анализа и предсказания в хаотических системах
Несмотря на непредсказуемость хаотических систем на длительных интервалах, существуют методы анализа и краткосрочного прогнозирования. Современные подходы комбинируют классические математические методы с машинным обучением и искусственным интеллектом.
Реконструкция фазового пространства
Метод временных задержек (метод Такенса) позволяет восстановить динамику системы по одномерному временному ряду. Этот подход критически важен для анализа реальных данных, где доступна информация только об одной переменной системы.
Основные этапы реконструкции:
- Выбор оптимальной размерности вложения
- Определение временной задержки через анализ автокорреляции
- Построение векторов состояния в многомерном пространстве
- Анализ топологических свойств восстановленного аттрактора
Современные методы прогнозирования
Краткосрочное прогнозирование хаотических систем возможно с использованием следующих подходов:
- Локальное линейное прогнозирование: Аппроксимация нелинейной динамики линейными моделями в окрестности текущего состояния
- Нейронные сети: Рекуррентные архитектуры (LSTM, GRU) эффективно захватывают нелинейные зависимости
- Reservoir Computing: Специализированный подход для динамических систем с использованием эхо-состояний
- Ансамблевые методы: Комбинирование множества прогнозов для повышения точности и оценки неопределенности
Оценка предсказуемости систем
Горизонт предсказуемости хаотической системы определяется обратной величиной максимального показателя Ляпунова. Для практических целей используются следующие метрики:
Время предсказуемости T ≈ (1/λ) × ln(δmax/δ₀)
где δmax — допустимая погрешность прогноза, δ₀ — точность измерений, λ — показатель Ляпунова.
Практические применения теории хаоса в Казахстане
Теория хаоса находит широкое применение в различных сферах экономики и науки Казахстана. От анализа финансовых рынков до прогнозирования погодных условий — понимание хаотической динамики помогает принимать более обоснованные решения в условиях неопределенности.
Финансовые рынки и экономическое моделирование
Казахстанская фондовая биржа (KASE) демонстрирует характерные признаки хаотического поведения. Анализ временных рядов индекса KASE Composite показывает наличие детерминированного хаоса с периодами относительной стабильности и резких изменений.
Применение методов теории хаоса в финансовом анализе включает:
- Определение горизонта прогнозирования для различных активов
- Выявление скрытых закономерностей в движении цен
- Оценка рисков на основе фрактальной размерности
- Построение адаптивных торговых стратегий
- Анализ влияния внешних шоков на рыночную динамику
Климатическое моделирование и метеорология
Казгидромет использует принципы теории хаоса для улучшения качества прогнозов погоды. Особенно это важно для континентального климата Казахстана с его резкими перепадами температур и непредсказуемыми осадками.
Ключевые направления применения:
- Ансамблевое прогнозирование: Использование множественных сценариев для оценки неопределенности
- Региональная детализация: Учет локальных особенностей климата различных областей
- Экстремальные события: Прогнозирование засух, наводнений и резких похолоданий
- Сельскохозяйственные приложения: Оптимизация сроков посева и уборки урожая
Нефтегазовая отрасль и геологическое моделирование
В нефтегазовой отрасли Казахстана теория хаоса применяется для моделирования сложных геологических процессов и оптимизации добычи углеводородов.
| Область применения | Методы | Результаты |
|---|---|---|
| Разработка месторождений | Фрактальный анализ пластов | Повышение коэффициента извлечения на 5-15% |
| Сейсморазведка | Хаотическая инверсия | Улучшение качества интерпретации |
| Транспортировка | Нелинейная динамика потоков | Оптимизация режимов перекачки |
| Экологический мониторинг | Анализ временных рядов | Раннее обнаружение аномалий |
Современные вычислительные методы и технологии
Развитие вычислительных технологий кардинально расширило возможности анализа хаотических систем. Современные суперкомпьютеры и специализированное программное обеспечение позволяют исследовать сложные многомерные системы, недоступные для аналитического решения.
Машинное обучение в анализе хаоса
Искусственный интеллект революционизирует подходы к изучению хаотических систем. Глубокие нейронные сети способны выявлять скрытые закономерности в данных, которые не поддаются традиционному математическому анализу.
Основные направления развития:
- Физически-информированные нейронные сети (PINNs): Интеграция известных физических законов в архитектуру нейронных сетей
- Генеративные модели: Создание синтетических данных для изучения редких событий
- Reinforcement Learning: Обучение управлению хаотическими системами через взаимодействие со средой
- Трансформеры для временных рядов: Использование механизма внимания для анализа долгосрочных зависимостей
Квантовые вычисления и хаос
Квантовые компьютеры открывают новые возможности для моделирования хаотических систем. Квантовый параллелизм позволяет исследовать экспоненциально большие пространства состояний, недоступные классическим компьютерам.
Перспективные применения включают:
- Квантовое моделирование многочастичных систем
- Оптимизация в хаотических ландшафтах
- Квантовые алгоритмы машинного обучения
- Исследование квантового хаоса
Облачные платформы и распределенные вычисления
Современные облачные сервисы предоставляют исследователям доступ к мощным вычислительным ресурсам без необходимости инвестиций в дорогостоящее оборудование. Это особенно важно для научных организаций Казахстана.
«Демократизация доступа к высокопроизводительным вычислениям через облачные технологии открывает новые горизонты для исследований в области теории хаоса» — отмечают эксперты Казахстанского национального университета имени аль-Фараби.
Философские и методологические аспекты
Теория хаоса не только изменила наше понимание физических и математических систем, но и оказала глубокое влияние на философию науки. Она поставила под сомнение классические представления о детерминизме и предсказуемости, открыв новые горизонты для понимания сложности окружающего мира.
Детерминизм против случайности
Одним из фундаментальных вопросов, поднимаемых теорией хаоса, является соотношение между детерминизмом и случайностью. Хаотические системы демонстрируют, что детерминированные процессы могут порождать поведение, неотличимое от случайного.
Это открытие имеет важные следствия:
- Пересмотр концепции причинности в сложных системах
- Ограничения научного метода в долгосрочном прогнозировании
- Новое понимание роли неопределенности в природе
- Философские вопросы о свободе воли и предопределенности
Редукционизм и холизм
Теория хаоса подчеркивает ограниченность редукционистского подхода, согласно которому понимание частей системы автоматически ведет к пониманию целого. Хаотические системы демонстрируют эмерджентные свойства, которые невозможно предсказать, изучая отдельные компоненты.
Холистический подход становится необходимым для понимания:
- Экосистем и биологического разнообразия
- Социально-экономических процессов
- Климатических изменений
- Функционирования головного мозга
- Эволюции сложных технических систем
Этические аспекты прогнозирования
Ограниченная предсказуемость хаотических систем поднимает важные этические вопросы о ответственности при принятии решений в условиях неопределенности. Это особенно актуально для политических и экономических решений, влияющих на жизнь миллионов людей.
Часто задаваемые вопросы о теории хаоса
Что такое теория хаоса простыми словами?
Теория хаоса изучает системы, где малейшие изменения могут привести к кардинально разным результатам. Представьте, что вы бросаете мяч с одной и той же силой, но каждый раз он отскакивает в совершенно разные стороны из-за микроскопических различий в поверхности или угле броска.
Можно ли предсказать хаотические системы?
Хаотические системы можно предсказывать только на короткие промежутки времени. Точность прогноза экспоненциально убывает со временем. Например, погоду можно прогнозировать с разумной точностью на 3-5 дней, но прогноз на месяц практически бесполезен.
В чем разница между хаосом и случайностью?
Хаос — это детерминированный процесс, который выглядит случайным. В хаотической системе каждое состояние строго определяется предыдущим по математическим законам, но поведение кажется непредсказуемым. Истинная случайность не имеет внутренних закономерностей.
Где в повседневной жизни встречается теория хаоса?
Теория хаоса проявляется повсюду: в погодных явлениях, колебаниях фондового рынка, динамике популяций животных, работе сердца, интернет-трафике, и даже в том, как формируется очередь в магазине. В Казахстане это особенно заметно в резких изменениях погоды и колебаниях цен на сырьевые товары.
Можно ли использовать хаос для получения выгоды?
Да, понимание хаотической динамики помогает в различных областях. В финансах — для управления рисками, в медицине — для диагностики аритмий, в технике — для создания более эффективных алгоритмов шифрования. Главное — не пытаться точно предсказать хаос, а использовать его статистические свойства.
Связана ли теория хаоса с квантовой механикой?
Теория хаоса и квантовая механика изучают разные типы неопределенности. Квантовая неопределенность фундаментальна и связана с природой измерений, в то время как хаос возникает из детерминированных, но нелинейных взаимодействий. Однако существует активная область исследований — квантовый хаос, изучающая пересечение этих концепций.
Как теория хаоса влияет на искусственный интеллект?
ИИ использует принципы теории хаоса для создания более робастных алгоритмов обучения, генерации случайных чисел, и анализа сложных данных. Хаотические нейронные сети могут избегать локальных минимумов и находить более креативные решения задач.
Будущее теории хаоса и перспективы развития
Теория хаоса продолжает активно развиваться, интегрируясь с новыми технологиями и научными направлениями. Современные тенденции указывают на расширение применимости хаотических методов в междисциплинарных исследованиях.